How do we identify transformations?

The 4 types of transformations are Rotations, Dilation, Reflection and Translation
Translation:
Every point is moved the same distance in the same direction.
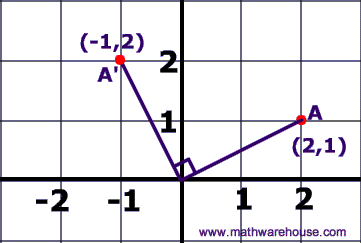
Reflection:
Figure is flipped over a line of symmetry.
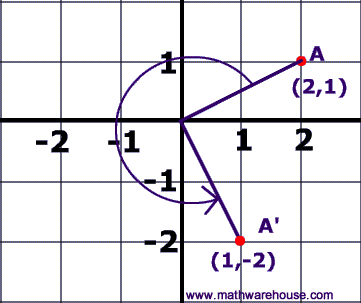
Rotation:
Figure is turned around a single point.
Dilation:
An enlargement or reduction in size of an image.
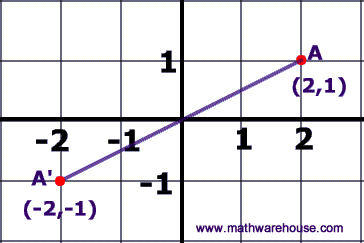
TRANSLATION:

Definition:  A translation (notation ) is a transformation of the plane that slides every point of a figure the same distance in the same direction.

Translations in the Coordinate Plane:

In the example below, notice how each vertex moves the same distance
 in the same direction.

In this next example, the "slide" (translation) moves the figure
7 units to the left and 3 units down.

DILATION

Example 1:

PROBLEM:  Draw the dilation image of triangle ABC with the center of  dilation at the origin and a scale factor of 2.OBSERVE: Notice how EVERY coordinate of the original triangle has been multiplied by the scale factor (x2). HINT: Dilations involvemultiplication!

http://www.regentsprep.org/Regents/math/geometry/GT3/Ldilate2.htmREFLECTION:

The reflection of the point (x, y) across the line y = x  is the point (y, x).       or       The reflection of the point (x, y) across the line y = -x  is the point (-y, -x).     or

http://www.regentsprep.org/Regents/math/geometry/GT3/Ldilate2.htm

http://www.regentsprep.org/Regents/math/geometry/GT2/Trans.htm

http://www.regentsprep.org/Regents/math/geometry/GT1/reflect.htm

How do we graph transformations that are the reflections?

Line Reflection:
(FLIP) A transformation that creates a figure which are mirror images.
Rule for reflection in the:
x-axis: (x,y) --- (x,-y)
y-axis: (x,y) --- (-x,y)

Reflecting over any line:

Each point of a reflected image is the same distance from the line of reflection as the corresponding point of the original figure.  In other words, the line of reflection lies directly in the middle between the figure and its image -- it is the perpendicular bisector of the segment joining any point to its image.  Keep this idea in mind when working with lines of reflections that are neither the x-axis nor the y-axis.

http://www.regentsprep.org/regents/math/geometry/GT1/reflect.htm

How do we graph rotations?

 A rotation is a transformation that turns the figure around the fixed point or the origin . When you want to rotate and don't want to use the entire word rotation you can just write capital R then degrees in the lower right bottom of the letter R. 
Remember: 
R is for rotation (ex: R90) &
r is for reflection (ex: ry-axis)
Rotation rules:
90 degrees = (x,y) --- (-y,x)
180 degrees = (x,y) --- (-x,-y)
270 degrees = (x,y) --- (-y.x)

• Rotation by 90° about the origin: R_{(origin, 90°)}

  A rotation by 90° about the origin can be seen in the picture below in which A is rotated to its image A'. The general rule for a rotation by 90° about the origin is (A,B) (-B, A)

2) Rotation by 180° about the origin: R_{(origin, 180°)}

A rotation by 180° about the origin can be seen in the picture below in which A is rotated to its image A'. The general rule for a rotation by 180° about the origin is (A,B) (-A, -B)

3) Rotation by 270° about the origin: R_{(origin, 270°)}

A rotation by 270° about the origin can be seen in the picture below in which A is rotated to its image A'. The general rule for a rotation by 270° about the origin is (A,B) (B, -A)

http://www.mathwarehouse.com/transformations/rotations-in-math.php

How do we identify composition of transformations?

Composition of transformation
When two or more transformations are combined to form a new transformation, the result is called a composition of transformations.







Ex:

http://regentsprep.org/Regents/math/geometry/GT6/composition.htm

How do we use the other definitions of transformations?

Glide Reflection:
A combination of a reflection in a line and a translation  along the line.
Orientation:
Orientation refers to the arrangement of points relative to one another, after a transformation has occurred.
Isometry:
An isometry is a transformation of the plane that preserves length.
Invariant:
A figure of property that remains unchanged under a transformation of the plane is referred to as invariant . No variations have occurred.
Translation:
Orientation size (isometry)

How do we solve logic problems using conditionals?

Ex:
Two angles are congruent( hypothesis)
Two angles are both right angles(conclusion)
 Then you just combine them and create one sentence by creating the inverse....
"if two angles are not congruent, then the two angles are not right triangles"

When the conditional and  converse are both true is it called a bi-conditional
Ex: " Next month is September if and only if this moth is August"
Contrapositive:
Contra - prefix meaning "against" or "opposite"
 So just negate and switch the hypothesis and conclusion ( inverse and converse)
Ex: " If i study, then i'll pass geometry"
Ans: "If  i did not pass geometry,then i did not study"

How do we find the locus of points?

The locus is the set of all points that satisfy a given condition, a  locus is a general graph of a given equation.

One Point:
What is the locus of points equidistant from one point?
The locus of points equidistant from a single point is a set of points equidistant from the next point in every direction.
Two Points:
What is the locus of points equidistant from two points?
The locus of points equidistant from two points is the perpendicular bisector of the line segment, connecting the two points.
One Line:
What is the locus of points equidistant from one line?
The locus of points equidistant from a line are two lines on opposite sides equidistant and are parallel in every direction.
Two Parallel Lines:
What is the locus of points equidistant from two parallel lines?
The locus of points equidistant from two parallel lines is another line half-way between both lines and parallel to each of them.
Two Intersecting Lines:
What is the locus of points equidistant from two intersecting lines?
The locus of points equidistant from two intersecting lines are two additional lines that bisect the angles formed by the original lines.